How Mathematics Helps Us Choose the Perfect Book

Our book club doesn't just vote on books — we use math to make sure the choices are fair, balanced, and loved by the group. This post dives into how we apply a Bayesian average to rank books using both internal preferences and external ratings from the Hardcover API.

Why Use a Formula to Pick a Book?

Choosing a book for a group can be surprisingly tricky. Some members prioritize popularity, others want quality reviews, and everyone wants their voice heard. To balance all of this, we use a formula that weighs:

• Average rating from the Hardcover API
• Number of external reviews
• Internal votes within our book club

The Bayesian Formula at Work

We use a Bayesian average to avoid over-rewarding books with a few high ratings and to reward those that have both quality and quantity. Here's how it's calculated:

def get_suggestion_score(self, hardcover_info=None):
    import math
    from flask import current_app

    C = 3.5  # Prior mean rating
    m = 10   # Prior weight (how many ratings to trust the prior)
    alpha = 0.7
    beta = 1 - alpha

    if hardcover_info:
        R = hardcover_info.get('rating')
        v = hardcover_info.get('rating_count', 0)
    else:
        R = self.num_stars
        v = m / 2  # fallback estimate

    votes = self.num_votes or 0

    bayesian_score = (v / (v + m)) * R + (m / (v + m)) * C if R and v else C
    vote_score = math.log(1 + votes)

    return alpha * bayesian_score + beta * vote_score

What This Means for the Club

This score balances popularity with group preference:

• Bayesian rating: reflects quality and review count
• Vote log score: makes sure club members’ input matters

Books that are loved externally and supported internally rise to the top — making it more likely everyone will be happy with the selection.

Example: How It Works

Imagine Book A has a 4.8 star rating on Hardcover with 3 ratings and 1 vote in the club.

Using our formula:

• R = 4.8 (Hardcover rating)
• v = 3 (number of Hardcover ratings)
• C = 3.5 (prior mean rating)
• m = 10 (prior weight)
• votes = 1

First we compute the Bayesian score:

bayesian_score = (3 / (3 + 10)) * 4.8 + (10 / (3 + 10)) * 3.5
               ≈ (0.23) * 4.8 + (0.77) * 3.5
               ≈ 1.104 + 2.695
               = 3.799

Then we compute the vote score:

vote_score = log(1 + 1) = log(2) ≈ 0.693

Finally, combine the scores using weights α = 0.7 and β = 0.3:

suggestion_score = 0.7 * 3.799 + 0.3 * 0.693
                 ≈ 2.659 + 0.208
                 = 2.867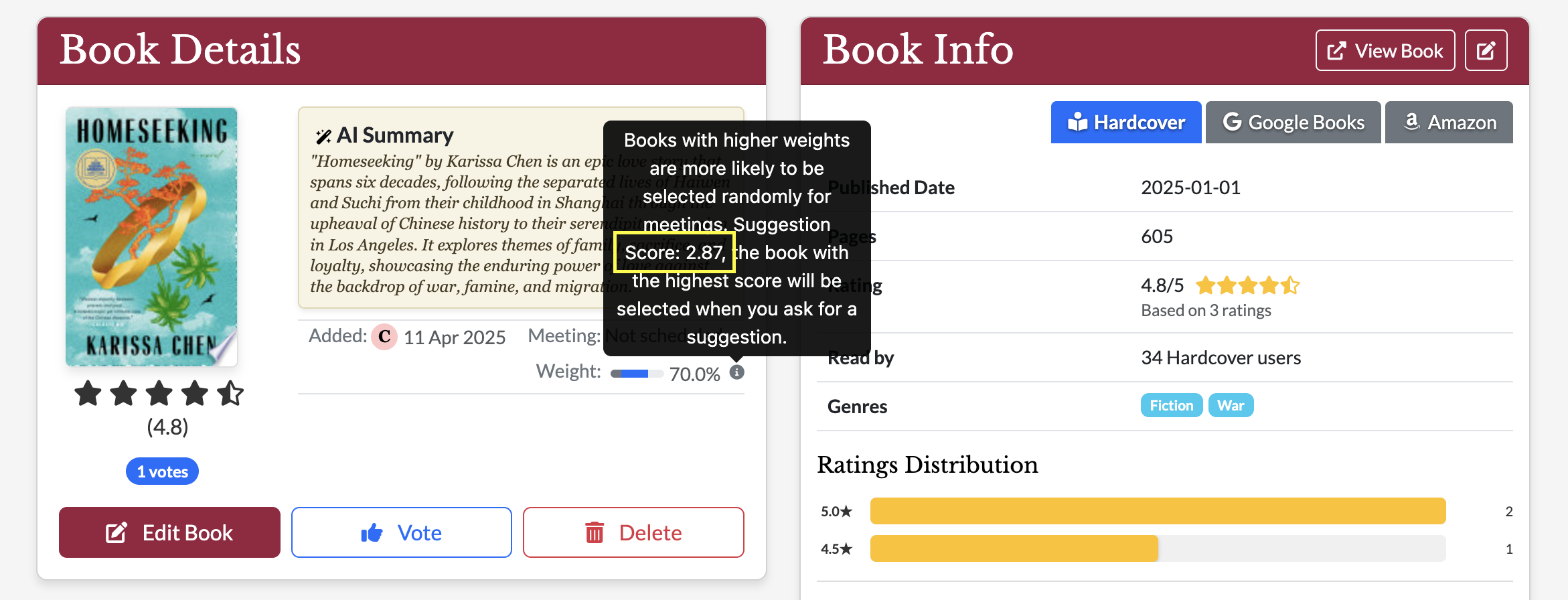

This score can now be compared to other books — even if they have more votes or different ratings — to help surface the best option.

In this way, we ensure that our book club selections are not just random or based on a single opinion, but rather a well-rounded choice that reflects both external popularity and internal preferences.

Conclusion

Combining data from the Hardcover API with internal votes and applying Bayesian mathematics allows us to make smarter book selections. It’s one more way we keep our book club running smoothly and our members satisfied.